Before all, if you’ve ever heard of hierarchical modeling (HLM), multilevel modeling (MLM), or mixed-effects model… they all mean the same thing! I use HLM and MLM interchangeably, and I hope people don’t get too confused by the messy terms.
Why HLM?
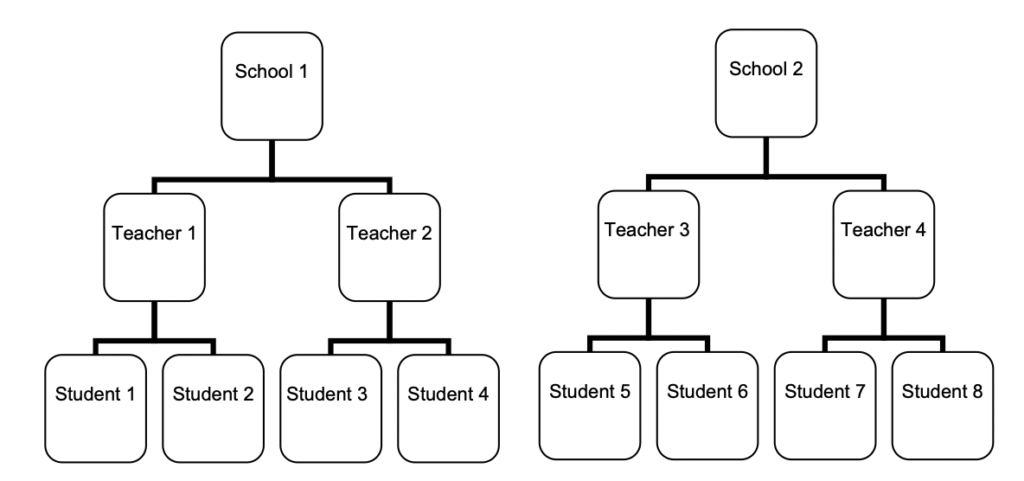
In practice, it’s common that your data isn’t randomly distributed. You may have participants giving similar responses because they are neighbors, or get highly correlated responses. Data is clustered, and your observations aren’t independent. That’s a big issue.
Let’s look at an example. Say you collected students’ math scores from a district. These students go to different schools. Within each school, they have different math teachers. The data is nested: students within teachers, and teachers within schools (See Fig 1).1 If you conduct a standard statistical test like ANOVA or simple linear regression, your results will be biased. This is because many standard tests require independent observations. If we ignore this nesting structure, students from the same school or taught by the same teacher will be treated as duplicates. It inflates your sample size and underestimates the standard error, leading to higher Type I Error rate. That is to say, even if your test is significant, the actual result is likely not significant at all.
“Why not get rid of the levels?” you might ask. Yes, we can take averages for each school, for example. By collapsing teachers and students, we turn data from 3-level to 1-level. However, the sample size will shrink a lot. It’s gonna reduce our statistical power, leading to higher Type II Error rates. That is to say, the actual result is significant, but we’re unlikely to discover that significance.
In addition, ignoring the nesting structure will end up with two conceptual errors: ecological fallacy and atomistic fallacy. Ecological fallacy means that your conclusion is about individuals (e.g., students), but it’s made based on group analysis (e.g., schools). Atomistic fallacy is that your conclusion is about the group, but it’s made based on individual analysis.
Why is this problematic? Suppose our results show that schools with more positive climate tend to have more sport events per year. If we conclude “students in positive-climate schools tend to do more sports”, we would commit ecological fallacy. Because individual students may not do sports at all, even if they are in a positive-climate school. Similarly, given that “students with higher self-efficacy are more likely to use AI”, we would commit atomistic fallacy if we say “schools with more confident students tend to have higher AI integration”. We can’t generalize students’ behavior to schools.
The interpretation of one level doesn’t automatically transfer to the another level. If we ignore that nesting structure, we can end up with committing one or both of these fallacies by attributing individual behaviors to groups, or vice versa.
Random Intercept Model (2-level)
We use HLM to remedy dependent observations. In short, HLM has two components: random effects and fixed effects. A slope and an intercept can either be random or fixed. Random effects vary across groups. Fixed effects is about the population.
In simple linear regression, both slope and intercept are fixed. In HLM, we can either to 1) set a random intercept or 2) set both random intercept and random slope. We typically don’t set random slopes alone, unless you have a very good reason to do so. 99% percent of the time, if you data have random slopes, it very likely has random intercepts as well.
It may help if we look at Fig 2.2 We see parallel regression lines, each is for a group. Intercept varies across groups, and the slope stays fixed. The figure shows the simplest form of HLM: random intercept model (RIM).
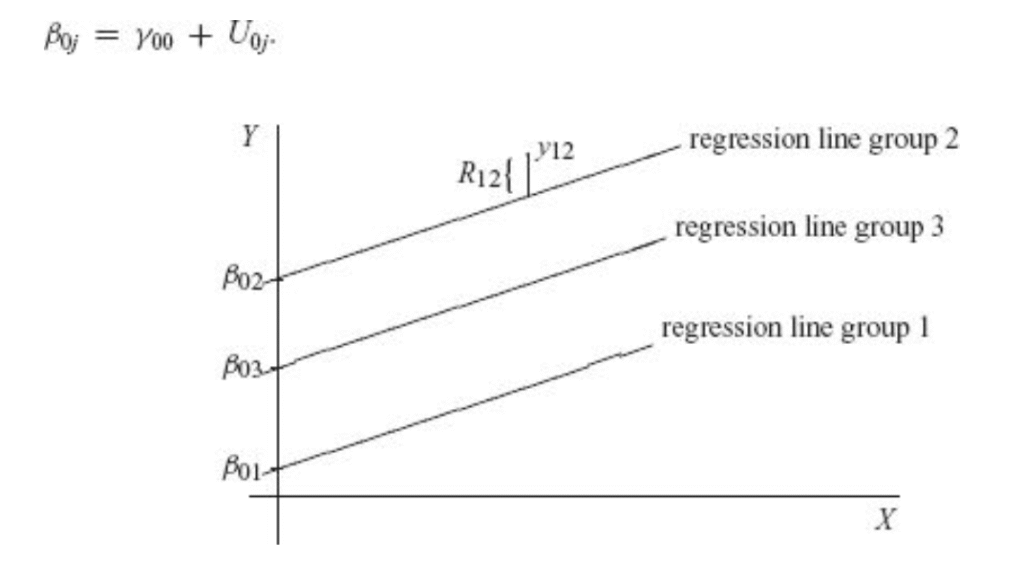
RIM has a random intercept and a fixed slope. In this example, our RIM incorporates two levels of data. Level 1 is about individual students. Level 2 is about schools. RIM captures the deviation of group means from the population grand mean. Let’s look at the null model:3
$$\text{Level 1: } Y_{ij} = \beta_{0j} + r_{ij} \text{ , } r_{ij} \sim N(0, \sigma^2)$$
$$\text{Level 2: } \beta_{0j} = \gamma_{00} + u_{0j} \text{ , } u_{0j} \sim N(0, \tau_0^2)$$
or if we combine the terms together,
$$Y_{ij} = \gamma_{00} + u_{0j} + r_{ij} \text{ , } r_{ij} \sim N(0, \sigma^2) \text{ , } u_{0j} \sim N(0, \tau_0^2)$$
where
- $i=(1…n_j)$ denotes the individual index for each group; $j=(1…J)$ denotes the group index.
- $\beta_{0j}$ is the average outcome for the $j$th group.
- $\gamma_{00}$ is the population grand mean; fixed intercept.
- $u_{0j}$ is the random deviation of group mean for the $j$th group from the population grand mean $(\gamma_{00})$; random intercept.
- $\tau_0^2$ is the between-group variance for level 2, indicating the variance of group means $(\beta_{0j})$.
- $r_{ij}$ is the residual of individual $i$ in group $j$.
- $\sigma^2$ is the within-group variance and is at level 1.
We can think of this as schools having different average math scores at baseline. Each school mean fluctuates around the population mean by $u_{0j}$. We capture the variance of that fluctuation, $\tau_0^2$ , to estimate the effect of schools on math scores. By summing $u_{0j}$ and population grand mean $(\gamma_{00})$, we get the random intercept $\beta_{0j}$ that varies across groups. Lastly, we add the residual $r_{ij}$ — an error term for each individual.
So, we have 3 parameters to estimate in RIM: $\gamma_{00}$, $\tau_0^2$, and $\sigma^2$. In HLM, when we say $\gamma$, it’s always a fixed constant. When we say $u$, it always has a random distribution. Each key parameter represents a question we want to ask:
- $\gamma_{00}$: What do we know about the average math score for the population?
- $\tau_0^2$: How do average math scores for schools vary?
- $\sigma^2$: How do math scores of students vary?
Similarly, for RIM with predictor $x$, it can be written as:
$$\text{Level 1: } Y_{ij} = \beta_{0j} + \beta_{1j}x_{ij} + r_{ij} \text{ , } r_{ij} \sim N(0, \sigma^2)$$
$$\text{Level 2: } \beta_{0j} = \gamma_{00} + u_{0j} \text{ , } u_{0j} \sim N(0, \tau_0^2) \text{ ; } \beta_{1j} = \gamma_{10}$$
or equivalently,
$$Y_{ij} = \gamma_{00} + \gamma_{10}x_{ij} + u_{0j} + r_{ij} \text{ , } r_{ij} \sim N(0, \sigma^2) \text{ , } u_{0j} \sim N(0, \tau_0^2)$$
where the new term $\gamma_{10}$ is the fixed slope between $Y_{ij}$ and $x_{ij}$ shared by all groups. By fixing the slope, we assume that 1-unit increase in $x_{ij}$ have the same effect on the increase in students’ math scores for each school. Nothing new going on here. The intercept still varies, and the slope of $x$ is fixed for all schools.
For the model above, we have the following assumptions:
- Linear relationship between $Y_{ij}$ and $x_{ij}$
- Independence between $u_{0j}$ and $r_{ij}$
- $u_{0j} \sim N(0, \tau_0^2)$; $u_{0j}$ is independent across schools
- $r_{ij} \sim N(0, \sigma^2)$
These assumptions are useful because they will help us calculate and interpret intraclass correlation, which I will discuss in the next section.
Intraclass Correlation
To check whether to use an HLM on your data, we estimate the intraclass correlation (ICC). If ICC is high enough (based on the criteria in your field), that indicates sufficient group-level variance compared to the total variance. Then, we choose to use HLM.
ICC ranges from 0 to 1. If ICC is super high, it means that the variance is entirely due to schools, instead of individual differences in students. If ICC is super low, we can ignore the school effect and give up HLM — just fit a simple linear regression instead. Different fields have different consensus for a large ICC. In education, ICC of 0.2 can be high enough to suggest a multilevel structure, but this may not be enough in other fields.
Generally, ICC has two interpretations:
- The proportion of variance accounted by groups.
- e.g., 28% of the variance is accounted for by the school students attend.
- The correlation between outcomes of two randomly selected individuals in the same randomly selected group.
- e.g., for two students attending the same school, the correlation between their math scores is 0.28.
In a two-level context, if we see ICC as the proportion of between-school variance, it can be written as:
$$\text{ICC} = \frac{\text{between-group variance}}{\text{total variance}} = \frac{\text{Var}(u_{0j})}{\text{Var}(u_{0j}+r_{ij})} = \frac{\tau_0^2}{\tau_0^2 + \sigma^2}$$
If we see ICC as how resemble two students from the same school are, we can write:
$$\rho(Y_{ij},Y_{i’j}) = \frac{\text{Cov}(Y_{ij},Y_{i’j})}{\text{SD}(Y_{ij})\text{SD}(Y_{i’j})} = \frac{\text{Cov}(u_{0j}+r_{ij}, u_{0j}+r_{i’j})}{\sqrt{\text{Var}(u_{0j}+r_{ij})}\sqrt{\text{Var}(u_{0j}+r_{i’j})}} =\frac{\text{Cov}(u_{0j}, u_{0j})}{\sqrt{\tau_0^2 + \sigma^2} + \sqrt{\tau_0^2 + \sigma^2}}=\frac{\tau_0^2}{\tau_0^2 + \sigma^2}$$
Let’s recall the assumptions of HLM. Since $r_{ij}$ is independent, and $u_{0j}$ and $r_{ij}$ are independent from each other, the covariance among $u_{0j}$, $r_{ij}$, and $r_{i’j}$ is all 0. We disregarded them when calculating $\text{Cov}(Y_{ij},Y_{i’j})$. Thus, the covariance between two students from the same school is $\text{Var}(u_{0j})$, the between-school variance. Both interpretations of ICC are correct. You can choose which one to use based on your research question.
Hypothesis Testing for Variance Component
After knowing if the data is multilevel, we still don’t know whether the multilevel structure matters in analysis. A simple model always more preferable than a complex one. Personally, I’d prefer a simple linear regression since it’s much less work! Hypothesis testing helps us see whether it’s worthy to keep random intercepts in our model. The null hypothesis is that the between-school variance is 0. The alternative hypothesis is that the between-school variance is greater than 0. In symbols, it writes as:
$$H_0: \tau_0^2=0 \text{ , } H_a: \tau_0^2 > 0$$
Essentially, we are wondering: is school randomness ($\tau_0^2$) large enough that we can use it to predict school means ($\beta_{0j}$)? If $\tau_0^2$ is close to 0 or when the sample size is large, we can just use the grand mean ($\gamma_{00}$) to predict school means. There is no need to fit an HLM! However, if $\tau_0^2$ is large enough, it will help us predict each school mean. Grand mean is no longer reliable since schools vary much from each other.
We can compare our RIM null model to a simple linear regression model by doing a likelihood ratio test (LRT). If the result is significant, we choose the more complex model (i.e., the RIM). In R, simply by running ranova(your_RIM), you will get useful comparisons of AIC (the lower the better) and LRT results.
Model Comparison
Similar to variance component testing, we can also use LRT to compare RIMs with different predictor specifications. Some fields use maximum likelihood estimates, but statisticians minimize things just to be safe. So, we look at a model’s deviance, defined as $D=-2logL$. In human words, deviance is “how bad the model fits”. So, we prefer models with a lower $D$ (badness).
Again, in LRT, by subtracting $D$ between reduced from the full model, we get a $\chi^2$ statistic. It means we check whether there is a difference in badness between the simpler model and the more complex model. If they are no different, we keep the simple model — RIM with less predictors. By running anova(RIM1, RIM2, RIM3), you can choose the best model by comparing the AICs, BICs, deviance, and p-values. All of them are useful criteria in comparing models.
In future posts, I will talk about random slope models and 3-level models. The equations and interpretations will be very ugly (I cried when I learned it the first time), but I’ll try my best to explain things more intuitively. Thanks for reading.
- Noell, G.H., Porter, B.A., & Patt, M.J. (2007). Value Added Assessment of Teacher Preparation in Louisiana: 2004 – 2006. ↩︎
- Snijders, T. A. B., & Bosker, R. J. (2012). Multilevel analysis: An introduction to basic and advanced multilevel modeling(2. ed). SAGE. ↩︎
- a.k.a. empty model or unconditional model — a default model with no additional predictors. ↩︎
